Question

A cross shaped pattern is made by arranging four identical rectangles around the sides of a square. The area of the square is 36cm2. The area of each rectangle is one and a third times the size of the square

Answer 1

88cm

Explanation:

The complete question is to Find the perimeter of the cross-shaped pattern.

See attachment for the figure.

If the area of the square is 36cm² , then the side length will be

s=√36=> 6cm

->If the area of each rectangle is one and a third times the area of the square

`1(1)/(3)` x 36 = 48cm²

breadth of each rectangle will be equal to the side length of the square i.e 6 cm, we will have

length x breadth = Area

length x 6 = 48

length = 8cm

Next is to find the perimeter. According to the figure, the perimeter will be

P= 4 x perimeter of rectangle - perimeter of square

P= 4 x 2(8+6) - (4 x 6) => 4 x 2(14) -24

P=88cm

Therefore, the perimeter of the cross-shaped pattern is 88cm

Answer 2

Area of a square is length * length

Area of a rectangle is length * breadth

In the question, the area of the square is 36

And the area of the rectangle is
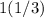`1(1/3)` the area of the square

To find the area of the rectangle, multiply 1(1/3) by the area of the square(36)

Area of rectangle becomes, 1(1/3) * 36 = (4/3) * 36 = 48cm2

To find the perimeter of the shape, we must find the perimeter of the rectangle - perimiter of the square

Since area of square is length * length, the length of the square is 6cm

The breadth of the rectangle is equal to the length of the square, hence, b = 6cm

Since, length * breadth = 48

l * 6 = 48

l = 8

Perimeter of the shape = 4 * perimeter of rectangle - perimter of square

Perimeter of rectangle = 2(l+b)

Perimeter of sqaure = 4l

Our answer = 4 * 2(6+8) - 4(6)

= 4 * 28 - 36

= 88cm

Explanation: