Question

Which of the following is a root of the polynomial function below

F(x)= x^3 - 3x^2 + x + 5
A) 2+I
B) 1
C) 2
D)-2+i

Answer 1

A) 2 + i

Explanation:

F(x) = x^3 - 3x^2 + x + 5

0 = x^3 - 3x^2 + x + 5

0 = (x+1)(x^2 - 4x + 5)

Great, now we can separate these two parenthesis expressions because of the Zero Product Property. Start with the simple one:

0 = x + 1

x = -1

We have our first real root! But it doesn't look like that's one of the answer choices, so move on to the other expression:

0 = (x^2 - 4x +5)

This expression can't be factored, so we will use the quadratic formula (which is x =
`\frac{-b+-\sqrt{b^(2)-4ac } }{2a}`).

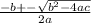First solve for the positive part:

= (4 + sqrt(16-20)) / 2

= 4 + sqrt(-4) / 2

= 4 + 2i / 2

= 2 + i

Then for the negative part:

= (4 - sqrt(16-20)) / 2

= 4 - sqrt(-4) / 2

= 4 - 2i / 2

= 2 - i

2 + i is answer choice A! Our other roots, 2 - i and -1, aren't answer choices.