Question

Construct a​ 95% confidence interval for the population​ mean, mu. Assume the population has a normal distribution. A random sample of 16 lithium batteries has a mean life of 645 hours with a standard deviation of 31 hours. Round to the nearest tenth.

Answer 1

Given Information:

Number of lithium batteries = n = 16

Mean life of lithium batteries = μ = 645 hours

Standard deviation of lithium batteries = σ = 31 hours

Confidence level = 95%

Required Information:

Confidence Interval = ?

Answer:

`CI = 628.5 \: to \: 661.5 \: hours`

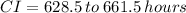
Step-by-step explanation:

The confidence interval is given by

`CI = \mu \pm t_(\alpha/2) ((\sigma)/(√(n)))`

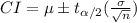
Where μ is the mean life of lithium batteries, σ is the standard deviation, n is number of lithium batteries selected, and t is the critical value from the t-table with significance level of

tα/2 = (1 - 0.95) = 0.05/2 = 0.025

and the degree of freedom is

DoF = n - 1 = 16 - 1 = 15

The critical value (tα/2) at 15 DoF is equal to 2.131 (from the t-table)

`CI = 645 \pm 2.131((31)/(√(16)))`

`CI = 645 \pm 2.131(7.75})`

`CI = 645 \pm 16.515`

`CI = 645 - 16.515 \: and \: 645 + 16.515`

`CI = 628.5 \: to \: 661.5 \: hours`

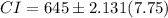
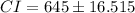
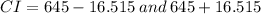
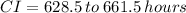
Therefore, the 95% confidence interval is 628.5 to 661.5 hours

What does it mean?

It means that we are 95% confident that the mean life of 16 lithium batteries is within the interval of (628.5 to 661.5 hours)