Answer:
The correct answer is 0.5.
Explanation:
The probability of a spinner landing on the shaded part follows binomial distribution.
Equation to be used is P(r) =
![\left[\begin{array}{ccc}n\\r\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/49vtqj1ptqevil27oitcbr57jzpvrjsqkp.png) ×
×
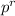 ×
×
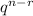 , where n is the number of times the spinner is spun and r is the number of times the spinner falls on the shaded region.
, where n is the number of times the spinner is spun and r is the number of times the spinner falls on the shaded region.
The probability of the spinner landing on the shaded part is p =
 . The probability of it landing on the unshaded part is q =
. The probability of it landing on the unshaded part is q =
 .
.
The spinner is spun n = 3 times.
We need to find the probability of it landing on the shaded part r = 2.
∴ Putting the values in the equation gives,
P(r) =
![\left[\begin{array}{ccc}3\\2\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/ftira6uft6ewudey5lb49hlxf917gl7fwa.png) ×
×
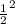 ×
×
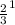 = 3 ×
= 3 ×
 ×
×
 = 0.5
= 0.5