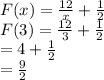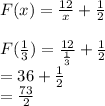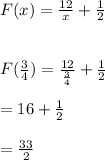Question

The function F is defined by F(x)= 12/x + 1/2 . Use this formula to find the following values of the function.

F(3)
F(−12)
F( 1/3 )
F( 3/4 )

Answer 1

Explanation:

Substitute in each value for x: F(x) becomes F(3)=12/3+1/2=2

Answer 2

`F(3)=(9)/(2) \\F(-12)=(-1)/(2) \\F((1)/(3) )=(73)/(2) \\F((3)/(4) )=(33)/(2)`

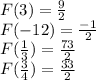
Explanation:

Given:
`F(x)= (12)/(x) + (1)/(2)`

To find: Values of the function F(3) , F(−12) ,
`F((1)/(3))`,
`F((3)/(4))`

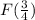
Solution:

A function is a relation in which each and every element of the domain has a unique image in the co-domain.

To find the values of the functions
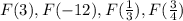`F(3),F(-12),F((1)/(3) ),F((3)/(4) )`, put
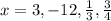`x=3, -12, (1)/(3),(3)/(4)` in the given function
`F(x)= (12)/(x) + (1)/(2)`

`F(x)= (12)/(x) + (1)/(2)\\F(3)= (12)/(3) + (1)/(2)\\=4 + (1)/(2)\\=(9)/(2)`

`F(x)= (12)/(x) + (1)/(2)\\F(-12)= (12)/(-12) + (1)/(2)\\=-1+(1)/(2)\\ =(-1)/(2)`

`F(x)= (12)/(x) + (1)/(2)\\\\F((1)/(3) )= (12)/((1)/(3)) + (1)/(2)\\=36+(1)/(2)\\ =(73)/(2)`

`F(x)= (12)/(x) + (1)/(2)\\\\\\F((3)/(4) )= (12)/((3)/(4)) + (1)/(2)\\\\=16+(1)/(2)\\ \\=(33)/(2)`