Question

Markus sent a chain letter to his friends, asking them to forward the letter to more friends. The relationship between the elapsed time, t tt, in days, since Markus sent the email, and the total number of people who receive the email, P ( t ) P(t)P, left parenthesis, t, right parenthesis, is modeled by the following function: P(t)=6⋅(1.43)t Complete the following sentence about the daily percent change in the number of people who receive the email. Every day, % %percent of people are added to / subtracted from the total number of people who receive the email.

Answer 1

Every day, 43% percent of people are added from the total number of people who receive the email

Explanation:

we know that

The equation of a exponential growth function is given by

`P(t)=a(1+r)^t`

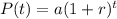
where

P(t) is the total number of people who receive the email

t is the time in days

a is the initial value

r is the rate of change

we have

`P(t)=6(1.43)^t`

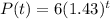
so

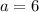`a=6` ---> initial number of people who receive the email

`(1+r)=1.43`

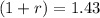
solve for r

`r=1.43-1\\r=0.43`

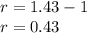
Convert to percentage

`0.43(100)=43\%`

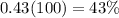
so

The daily percent change in the number of people who receive the email. every day is 43%

therefore

Every day, 43% percent of people are added from the total number of people who receive the email