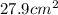Answer:
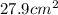
Explanation:
The total area of the circle is given by:
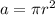
where
 is a constant
is a constant
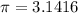
and
 is the radius:
is the radius:
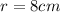
Thus the total area of this circle is:
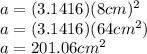
We want only the area of the arc that measures 50°. For this we must remember that the arc of the total circle is 360°.
Thus, we want 50° out of the 360° degrees in the circle. For this, we divide the total area by 360 and then we multiply by 50:
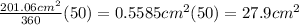
the area of the sector to the nearest tenth is