Question

Find the equation of the line that passes through the points (-5,7) and (2,3)

Answer 1

`y=-(4)/(7)x+4(1)/(7)`

Explanation:

So, in order to solve this problem, I started off by drawing it out. On my graph that I have attached below, I first started out by locating the points (-5,7) and (2,3). Now, this is an optional step, but I highly encourage practicing your graphing skills by solving this problem on graph paper as well. Next, I connected the two points that I just graphed. This is the line that passes through (-5,7) and (2,3).

Now, here is where the actual solving starts. If you haven't already been taught this yet, I will introduce it to you now. I am going to find the equation of this line by filling in what I know in the equation y=mx+b, where m= the slope of the line, and b= y intercept.

Slope of the line: m=
`(y_(1) - y_(2) )/(x_(1) - x_(2) ) = (7-3)/(-5-2) = (4)/(-7)= -(4)/(7)`

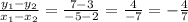
If you haven't been taught how to find the slope of a line I recommend you find out.

Substitute the slope into the equation.

`y=-(4)/(7) x+b\\`

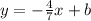
Now, we will solve for the 'b,' or y intercept.

We already have x and y values to use: (-5,7) or (2,3). I'll use x=2 and y=3 to solve for the y intercept.

`y=-(4)/(7) x+b\\\\3=-(4)/(7) *2+b\\\\3=-(8)/(7) +b\\b=3+(8)/(7) \\b=(21)/(7)+(8)/(7)=(29)/(7) =4(1)/(7) \\b=4(1)/(7)`

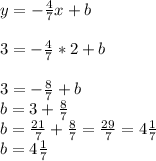
Last step: substitute the slope and y intercept into y=mx+b.

`y=mx+b\\y=-(4)/(7)x+4(1)/(7)`

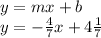
That is the answer to this problem.

I hope this helps.