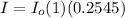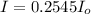Question

(a) How many fringes appear between the first diffraction-envelope minima to either side of the central maximum in a double-slit pattern if λ = 471 nm, d = 0.117 mm, and a = 35.7 µm? (b) What is the ratio of the intensity of the third bright fringe to the intensity of the central fringe?

Answer 1

a

The number of fringe is z = 3 fringes

b

The ratio is
`I = 0.2545I_o`

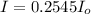
Step-by-step explanation:

a

From the question we are told that

The wavelength is
`\lambda = 600 nm`

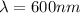
The distance between the slit is
`d = 0.117mm = 0.117 *10^(-3) m`

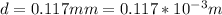
The width of the slit is
`a = 35.7 \mu m = 35.7 *10^(-6)m`

let z be the number of fringes that appear between the first diffraction-envelope minima to either side of the central maximum in a double-slit pattern is and this mathematically represented as

`z = (d)/(a)`

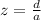
Substituting values

`z = (0.117*10^(-3))/(35.7 *10^(-6))`

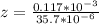
z = 3 fringes

b

From the question we are told that the order of the bright fringe is n = 3

Generally the intensity of a pattern is mathematically represented as

`I = I_o cos^2 [(\pi d sin \theta)/(\lambda) ][(sin (\pi a sin (\theta)/(\lambda ) ))/(\pi a sin (\theta)/(\lambda) ) ]`

Where
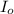`I_o` is the intensity of the central fringe

And Generally
`sin \theta = (n \lambda )/(d)`

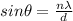
`I = I_o co^2 [ (\pi ((n \lambda)/(d) ))/(\lambda) ] [((sin (\pi a ((n \lambda)/(d) )))/(\lambda) )/((\pi a ((n \lambda)/(d) ))/(\lambda) ) ]`

`I = I_o cos^2 (n \pi)[((sin(\pi a ((n \lambda)/(d) )))/(\lambda) ))/( ( \pi a ((n \lambda )/(d) ))/(\lambda) ) ]`

`I = I_o cos^2 (3 \pi) [(sin ((3 \pi )/(6) ))/((3 \pi)/(6) ) ]`

`I = I_o (1)(0.2545)`

`I = 0.2545I_o`