Question

Each of the following situations describes a normally distributed population for which a statistical procedure should be used. Match each situation with the appropriate procedure to use.

a) Gale is obsessed with creating a reliable method of brewing the perfect cup of coffee. She wants to determine the likely range of weight of whole coffee beans from her trusty two-tablespoon scoop. She measures the weight of a sample of 15 scoops, finding that they average 17 g.
b) Tanya is studying IQ scores, which are normally distributed with a mean of 100. She believes that the mean IQ of classical musical composers is at least 112 and tests this belief with a random sample of 20 composers.
c) Jason wants to estimate what the balance of his retirement account will be in one month. All of the money in his account is allocated in an S&P 500 Index Fund. From 1950 to 2015, he calculates this index has had an average monthly return of 0.69% with a standard deviation of 4.15%.
Procedure:
1. one sample t-confidence interval for a mean
2. one sample z-test for a mean
3. one sample t-test for a mean
4. one sample z-confidence interval for a mean

Answer 1

(a) Correct option (1).

(b) Correct option (3).

(c) Correct option (2).

Explanation:

A one-sample z-test for mean is used to determine whether the claimed value of mean is significant or not. To perform this test we can also use the t-distribution.

The t-test is used if the following conditions are given:

1. The population is normally distributed
2. The population standard deviation is not known
3. The sample selected is large enough.

Similarly the (1 - α)% confidence interval for population mean can be computed either using the z-interval or the t-interval.

The same conditions should be applied to use the t-interval.

(a)

In the first case, Gale wants to determine the likely range of weight of whole coffee beans from her trusty two-tablespoon scoop to create a reliable method of brewing the perfect cup of coffee.

She selects a sample of n = 15 scoops and perform the test.

Since the population standard deviation is not known and Gale wants to know the range of weight of whole coffee beans , she should use a one sample t-confidence interval for a mean.

The correct option is (1).

(b)

In the second case, Tanya wants to determine whether the mean IQ score is at least 112 or not.

She selects a a random sample n = 20 composers and compute the statistic to perform the one-sample test.

Since the population standard deviation is not known, Tanya should use one sample t-test for a mean.

The correct option is (3).

(c)

In the second case, Jason wants to estimate what the balance of his retirement account will be in one month.

He selects the data from 1950 to 2015 and calculates this index has had an average monthly return of 0.69% with a standard deviation of 4.15%.

Now, the sample selected is quite large. The Central limit theorem can be used to approximate the sampling distribution of sample mean.

Then,
`\bar X\sim N(\mu_(\bar x), \sigma_(\bar x))`

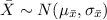
So, Jason can use the one sample z-test for a mean to determine the balance of his retirement account will be in one month.

The correct option is (2).