Question

If the Hubble Space Telescope is 598 m above the surface of the Earth and is traveling at 7.56 x 103 m/s, how long does it take the Hubble Space Telescope to orbit the earth? (Radius of the earth RE= 6.38 x 106 m, Mass of the earth ME = 5.98 x 1024 kg)

Answer 1

88.25822 Minutes

Step-by-step explanation:

`T=(S)/(V)` Relates T, time period To S, circumference at height of 598m and V velocity.

S = circumference =
`2\pi (h+r)=2\pi (598m+3.38*10^6)=40033930.94meters.`

Substituting all this in our equation gives.

`T = (40033930.94m)/(7.56*10^3m/s) =5295.49351s=88.25822minutes.`

Answer 2

5069.04 seconds

Step-by-step explanation:

The parameter we are looking for is called the Orbital period of the Hubble Space Telescope.

It is given as:

`T = \sqrt{(4\pi^2r^3 )/(GM) }`

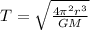
where r = radius of orbit of Hubble Space Telescope

G = gravitational constant =
`6.67408 * 10^(-11) m^3 kg^(-1) s^(-2)`

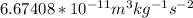
M = Mass of earth

We are given that:

r = radius of the earth + distance of HST from earth

r =
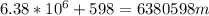
`6.38 * 10^6 + 598 = 6380598 m`

M =
`5.98 * 10^(24) kg`

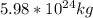
Therefore, T will be:

`T = \sqrt{(4*\pi^2 * 6380598^3 )/(6.67408 * 10^(-11) * 5.98 * 10^(24))}`

`T = 5069.04 secs`

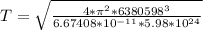
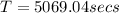
The orbital period of the Hubble Space Telescope is 5069.04 seconds.