Answer:
Probability that the mean service time is between 1 and 2 hours is 0.96764.
Explanation:
We are given that a systematic random sample of 100 service appointments has been collected.
The 100 appointments showed an average preparation time of 90 minutes with a standard deviation of 140 minutes.
Let
 = sample mean service time
= sample mean service time
The z-score probability distribution for sample mean is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = average preparation time = 90 minutes
= average preparation time = 90 minutes
 = standard deviation = 140 minutes
= standard deviation = 140 minutes
n = sample of appointments = 100
The Z-score measures how many standard deviations the measure is away from the mean. After finding the Z-score, we look at the z-score table and find the p-value (area) associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X.
Now, probability that the mean service time is between 60 and 120 minutes is given by = P(60 minutes <
 < 120 minutes)
< 120 minutes)
P(60 minutes <
 < 120 minutes) = P(
< 120 minutes) = P(
 < 120 min) - P(
< 120 min) - P(

 60 min)
60 min)
P(
 < 120 min) = P(
< 120 min) = P(
 <
<
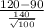 ) = P(Z < 2.14) = 0.98382
) = P(Z < 2.14) = 0.98382
P(

 60 min) = P(
60 min) = P(


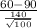 ) = P(Z
) = P(Z
 -2.14) = 1 - P(Z < 2.14)
-2.14) = 1 - P(Z < 2.14)
= 1 - 0.98382 = 0.01618
The above probability is calculated by looking at the value of x = 2.14 in the z table which has an area of 0.98382.
Therefore, P(60 min <
 < 120 min) = 0.98382 - 0.01618 = 0.96764
< 120 min) = 0.98382 - 0.01618 = 0.96764