Complete Question
The complete question is shown on the first uploaded image
Answer:
Step-by-step explanation:
From he question we are told that
The first mass is
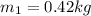
The second mass is
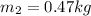
From the question we can see that at equilibrium the moment about the point where the string holding the bar (where
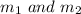 are hanged ) is attached is zero
are hanged ) is attached is zero
Therefore we can say that
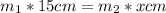
Making x the subject of the formula
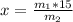
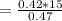

Looking at the diagram we can see that the tension T on the string holding the bar where
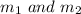 are hanged is as a result of the masses (
are hanged is as a result of the masses (
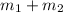 )
)
Also at equilibrium the moment about the point where the string holding the bar (where (
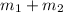 ) and
) and
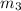 are hanged ) is attached is zero
are hanged ) is attached is zero
So basically
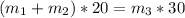

Making
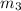 subject
subject

