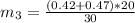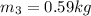Question

In the mobile m1=0.42 kg and m2=0.47 kg. What must the unknown distance to the nearest tenth of a cm be if the masses are to be balanced? The answer is 13.4 In the mobile what is the value for m3 to the nearest hundredth of a kilogram?

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

Step-by-step explanation:

From he question we are told that

The first mass is
`m_1 = 0.42kg`

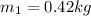
The second mass is
`m_2 = 0.47kg`

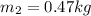
From the question we can see that at equilibrium the moment about the point where the string holding the bar (where
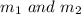`m_1 \ and \ m_2` are hanged ) is attached is zero

Therefore we can say that

`m_1 * 15cm = m_2 * xcm`

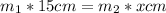
Making x the subject of the formula

`x = (m_1 * 15)/(m_2)`

`= (0.42 * 15)/(0.47)`

`x = 13.4 cm`

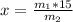
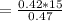
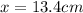
Looking at the diagram we can see that the tension T on the string holding the bar where
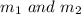`m_1 \ and \ m_2` are hanged is as a result of the masses (
`m_1 + m_2`)

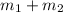Also at equilibrium the moment about the point where the string holding the bar (where (
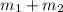`m_1 +m_2`) and
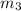`m_3` are hanged ) is attached is zero

So basically

`(m_1 + m_2 ) * 20 = m_3 * 30`

`(0.42 + 0.47) * 20 = 30 * m_3`

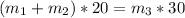
Making
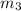`m_3` subject

`m_3 = ((0.42 + 0.47) * 20 )/(30 )`

`m_3 = 0.59 kg`