Answer:
Probability that their hair was done by Amy is 0.475.
Explanation:
We are given that Sally's Hair Salon there are three hair stylists. 36% of the hair cuts are done by Chris, 26% are done by Karine, and the rest are done by Amy.
Let the Probability of hair cutting done by Chris = P(C) = 0.36
Probability of hair cutting done by Karine = P(K) = 0.26
Probability of hair cutting done by Amy = P(A) = 0.368
Also, let NS = event that customer is not satisfied with his cutting
So, Probability that customers are not satisfied given that their hair cutting is done by Chris = P(NS/C) = 0.05
Probability that customers are not satisfied given that their hair cutting is done by Karine = P(NS/K) = 0.06
Probability that customers are not satisfied given that their hair cutting is done by Amy = P(NS/A) = 0.08
Now, a customer leaving the salon is selected at random. If the customer is not satisfied, the probability that their hair was done by Amy is given by = P(A/NS)
For finding the above probability we will use the concept of Bayes' Theorem;
SO, P(A/NS) =

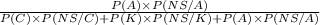
=

=
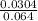
= 0.475
Hence, the probability that their hair was done by Amy is 0.475.