Question

Direct Mailing Company sells computers and computer parts by mail. The company claims that more than 90% of all orders are mailed within 72 hours after they are received. The quality control department at the company often takes samples to check if this claim is valid. A recently taken sample of 175 orders showed that 161 of them were mailed within 72 hours. Do you think the company’s claim is true? Use the 1% significance level. What type of problem is this?

Answer 1

We conclude that less than or equal to 90% of all orders are mailed within 72 hours after they are received which means the company's claim is not true.

Explanation:

We are given that the company claims that more than 90% of all orders are mailed within 72 hours after they are received. The quality control department at the company often takes samples to check if this claim is valid.

A recently taken sample of 175 orders showed that 161 of them were mailed within 72 hours.

Let p = percentage of all orders that are mailed within 72 hours.

SO, Null Hypothesis,
`H_0` : p
`\leq` 90% {means that less than or equal to 90% of all orders are mailed within 72 hours after they are received}

Alternate Hypothesis,
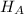`H_A` : p > 90% {means that more than 90% of all orders are mailed within 72 hours after they are received}

The test statistics that will be used here is One-sample z proportion statistics;

T.S. =
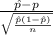`\frac{\hat p-p}{{\sqrt{(\hat p(1-\hat p))/(n) } } } }` ~ N(0,1)

where,
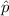`\hat p` = proportion of orders that were mailed within 72 hours in a sample of 175 =
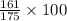`(161)/(175)* 100` = 92%

n = sample of orders = 175

So, test statistics =
`\frac{0.92-0.90}{{\sqrt{(0.92(1-0.92))/(175) } } } }`

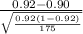
= 0.975

The value of the test statistics is 0.975.

Now at 1% significance level, the z table gives critical value of 2.3263 for right-tailed test. Since our test statistics is less than the critical value of z as 0.975 < 2.3263, so we have insufficient evidence to reject our null hypothesis as it will not fall in the rejection region due to which we fail to reject our null hypothesis.

Therefore, we conclude that less than or equal to 90% of all orders are mailed within 72 hours after they are received which means the company's claim is not true.