Question

You are asked to design a spring that will give a 1020 kg satellite a speed of 2.25 m/s relative to an orbiting space shuttle. Your spring is to give the satellite a maximum acceleration of 5.00g. The spring's mass, the recoil kinetic energy of the shuttle, and changes in gravitational potential energy will all be negligible.

(a) What must the force constant of the spring be?
(b) What distance must the spring be compressed?

Answer 1

To design a spring for a 1020 kg satellite to achieve a speed of 2.25 m/s with a maximum acceleration of 5.00g, one must calculate the spring constant (k) using the relationship between the satellite's kinetic energy and the spring's potential energy, and the maximum acceleration allowed. The compression distance (x) is then determined using the final velocity and maximum acceleration. Both k and x are computed ignoring the mass of the spring or any recoil kinetic energy from the shuttle.

Step-by-step explanation:

To solve for the force constant of the spring that will give a 1020 kg satellite a speed of 2.25 m/s relative to an orbiting space shuttle, we use the energy principle and Hooke's law. The maximum acceleration is 5.00g, which is 5 times the acceleration due to gravity (approximately 5 x 9.81 m/s²).

a. Calculating the force constant (k) of the spring:

• The kinetic energy (KE) imparted to the satellite is equal to the potential energy (PE) stored in the spring: KE = PE.
• KE = (½)mv², where m is the mass of the satellite, and v is the velocity.
• PE = (½)kx², where k is the spring constant, and x is the compression distance.
• Set KE equal to PE: (½)mv² = (½)kx².
• We also know that the maximum force Fmax provided by the spring (when compressed by distance x) equals the maximum acceleration (amax) times the mass m: Fmax = kx = amax*m.
• Using amax = 5g = 5 * 9.81 m/s², solve for k: k = Fmax / x = m * amax / x.
• However, x is not given, but we can find it using v² = 2 * amax * s, where s is the distance the satellite moves under constant acceleration (which equals x).
• Solving this for x gives us x = v² / (2 * amax).
• Substitute the value of x back into the expression for k.
• Finally, calculate k using the given mass and maximum acceleration.

b. Calculating the compression distance (x) of the spring:

• Use the value of amax and the final velocity v to find the displacement x as previously derived: x = v² / (2 * amax).
• Substitute the known values of v and amax to find x.

This approach allows us to determine both the force constant and the compression distance without the mass of the spring or the recoil kinetic energy of the shuttle affecting our calculations because they are negligible.

Answer 2

(a) 2.45×10⁵ N/m

(b) 0.204 m

Step-by-step explanation:

Here we have that to have a velocity of 2.25 m/s then the relationship between the elastic potential energy of the spring and the kinetic energy of the rocket must be

Elastic potential energy of the spring = Kinetic energy of the rocket

`(1)/(2) kx^2 = (1)/(2) mv^2`

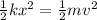
Where:

k = Force constant of the spring

x = Extension of the spring

m = Mass of the rocket

v = Velocity of the rocket

Therefore,

`(1)/(2) kx^2 = (1)/(2) * 1020 * 2.25^2`

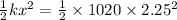
or

`kx^2 = 1020 * 2.25^2 = 10,226.25\\So \ that \ the \ force \ on \ the \ satellite\ kx = (10226.25)/(x)`

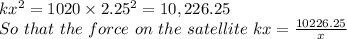
(b) Since the maximum acceleration is given as 5.00×g we have

Maximum acceleration = 5.00 × 9.81 = 49.05 m/s²

Hence the force on the rocket is then;

Force = m×a = 1020 × 49.05 = ‭50,031 N

`kx = (10226.25)/(x) = 50031 \ N`

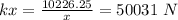
Therefore,

`x = (10226.25)/( 50031) = 0.204 \ m`

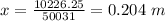
(a) From which

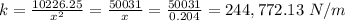`k = (10226.25)/(x^2) = (50031)/(x) = (50031)/(0.204) = 244,772.13 \ N/m` or

Force constant of the spring, k = 2.45×10⁵ N/m.