Answer:
At t = 3, pilot can hit the target located at the origin.
Explanation:
We have been given displacement vector:
r(t) = 5 - t, 21 - t², 3-t³/27
so, in this case r(t) and r'(t) should be in the parallel but opposite direction.
In order to get r'(t) we need to differentiate r(t).
r(t) = 5 - t, 21 - t², 3-t³/27
r'(t) = -1, -2t, -t²/9
Now perform the cross product among these two r(t) and r'(t).
r'(t) x r(t) =
![\left[\begin{array}{ccc}i&j&k\\-1&-2t&(-t^(2) )/(9) \\5-t&21-t^(2) &3-(t^(3) )/(27) \end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/ezr12egg9pt1ontsj7kemvjtkocjup7ai5.png)
= i ((-6t +
 )+ (
)+ (
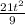 -
-
 )) -j ((-3 +
)) -j ((-3 +
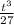 +
+
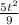 -
-
 )) + k ((-21 +
)) + k ((-21 +
 + 10t -2
+ 10t -2
 ))
))
= (
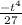 +
+
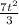 - 6t )i + (
- 6t )i + (
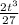 -
-
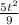 +3) j + (-t² + 10t -21)k
+3) j + (-t² + 10t -21)k
In order to find the value of t, we need to put
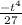 +
+
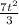 - 6t = 0
- 6t = 0
-t² + 10t -21 = 0
So, after solving for t, we will get
- ( t-3) (t-7) = 0
t = 3 or t = 7
In this case, only t = 3 satisfies the other two equations as well. t=7 is not satisfying. So take t =3 as the time. and for further assurance, we need to check are our vectors r(t) and r'(t) opposite at t = 3 or not. Let's check it out.
r(3) = 5-3, 21 - 3², 3 - 3³/27
r (3) = 2, 12, 2
r'(3) = -1, -2(3) , -3²/9
r'(3) = -1, -6 -1
Here, we can easily see that, r(3) = -2 r'(3) which is opposite and hence it is proved that, at exactly t = 3, pilot can hit a target located at the origin.