Answer:
YTM: 2.64%
YTC: 3.66%
Step-by-step explanation:
The market price is the discounted price of the maturity and coupon payment at market rate:
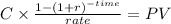
C 3.700
time 40
rate 0.013221404
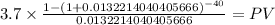
PV $114.3676
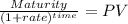
Maturity 100.00
time 40.00
rate 0.013221404
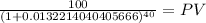
PV 59.13
PV c $114.3676
PV m $59.1324
Total $173.5000
Then we do the same calcaulation with the 161 call price being the maturity and adjusting time for 10 years (20 payment)
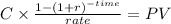
C 3.700
time 20
rate 0.018309924
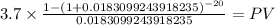
PV $61.4988
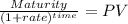
Maturity 161.00
time 20.00
rate 0.018309924
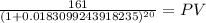
PV 112.00
PV c $61.4988
PV m $112.0021
Total $173.5009
Now we got the semiannual rate we simply multiply by two to convert into annual rates.
YTM:
0.013221404 X 2 = 0,026442808 = 2.64%
YTC:
0.0183099243918235 X 2 = 0,036619848783647 = 0.0366 = 3.66%