Answer:
3.89m
Step-by-step explanation:
To find the length of the pipe you can use the formula for the modes of the pipe with a closed end:
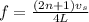
n: mode of frequency
vs : sound speed = 343m/s
L: length of the pipe
by taking the difference between two consecutive modes you obtain:
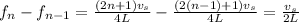
by using two consecutive frequencies in the previous expression and replacing you get:

hence, the length of the pipe is 3.89m