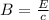Question

We can reasonably model a 90 W incandescent lightbulb as a sphere 5.2 cm in diameter. Typically, only about 5% of the energy goes to visible light; the rest goes largely to nonvisible infrared radiation.

A) What is the visible light intensity at the surface of the bulb?
B) What is the amplitude of the electric field at this surface, for a sinusoidal wave with this intensity?
C) What is the amplitude of the magnetic field at this surface, for a sinusoidal wave with this intensity?

Answer 1

(a)
`530W/m^2`

(b) 631.85 V/m

(c)
`210* 10^(-8)T`

Step-by-step explanation:

We have given power P = 90 watt

Diameter of the sphere d = 5.2 cm

So radius r = 2.6 cm = 0.026 m

(a) Intensity is equal to
`I=(P)/(A)=(P)/(4\pi r^2)`

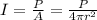
So
`I=(0.05* 90)/(4* 3.14* 0.026^2)=530W/m^2`

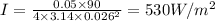
(b) Energy density is equal to

`u=(1)/(2)\epsilon _0E^2`

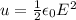
It is also known that
`u=(I)/(c)`

`(I)/(c)=(1)/(2)\epsilon _0E^2`

`E=\sqrt{(2I)/(\epsilon _0C)}`

`E=\sqrt{(2* 530)/(8.85* 10^(-12)* 3* 10^8)}=631.85V/m`

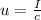
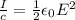
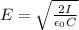
(c) Amplitude of magnetic field

`B=(E)/(c)`

`B=(631.85)/(3* 10^8)=210* 10^(-8)T`