Answer:
(a) Slightly greater than 20.0 °C
(b)
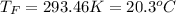
Step-by-step explanation:
Hello,
In this case, since we are talking about the equilibrium temperature that will be reached when the copper, chromium and water samples get in contact, the following equation is useful to describe such situation:
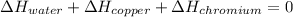
Thus, in terms of masses, heat capacities and temperatures we consider the final temperature as the unknown:
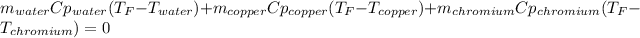 In such a way, by knowing that the heat capacities of copper and chromium are 0.386 and 0.45 J/(g°C) respectively, by solving for the equilibrium temperature one has:
In such a way, by knowing that the heat capacities of copper and chromium are 0.386 and 0.45 J/(g°C) respectively, by solving for the equilibrium temperature one has:
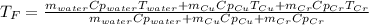
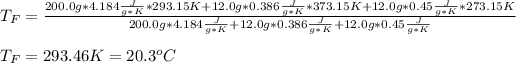
Hence, the resulting temperature of water turns out slightly greater than 20.0 °C.
Best regards.