Question

Radar uses radio waves of a wavelength of 2.2 m . The time interval for one radiation pulse is 100 times larger than the time of one oscillation; the time between pulses is 10 times larger than the time of one pulse. What is the shortest distance to an object that this radar can detect?

Answer 1

The shortest distance to an object that this radar can detect would be

111 m

Step-by-step explanation:

The shortest distance is the minimum distance that would be detected by the radar, The time of oscillation can be obtained thus;

T = 1/f ..........1

but f= v/λ substituting f into equation 1 we have;

T = λ/v...............2

Where λ is the wavelength = 2.2 m

v is the velocity of light since the radar is an electromagnetic wave

= 3 x
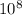`10^(8)` m/s

T = 2.2 m / 3 x
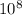`10^(8)` m/s

T = 7.33 x
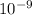`10^(-9)` s

Calculating the time interval required by the pulse

Since the interval of the pulse (t) is 100 times greater than the period of oscillation, the time of the pulse is expressed as;

t = 100 x T

t = 100 x 7.33 x
`10^(-9)` s

t = 7.33 x
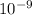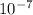`10^(-7)` s

Therefor the time of the pulse is 7.33 x
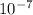`10^(-7)` s

Calculating for the shortest distance of the radar

The shortest distance of the radar can be obtained using the equation below;

λ_s = (t/2) x v ............3

Substituting into equation 3 we have

λ_s = (7.33 x
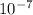`10^(-7)` /2) x 3 x
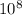`10^(8)` m/s

λ_s = 111 m

Therefore the shortest distance to an object that this radar can detect would be 111 m