Question

A city council is deciding whether or not to spend additional money to reduce the amount of traffic. The council decides that it will increase the transportation budget if the amount of waiting time for drivers exceeds 18 minutes. A sample of 26 main roads results in a mean waiting time of 21.1 minutes with a sample standard deviation of 5.4 minutes. Conduct a hypothesis test at the 5% significance level.

Answer 1

t = 2.9272 > 1.708 at 25 degrees of freedom

null hypothesis is rejected

The council decides that it will increase the transportation budget if the amount of waiting time for drivers is not exceeds 18 minutes

Explanation:

Step (i):-

A sample of 26 main roads results in a mean waiting time of 21.1 minutes with a sample standard deviation of 5.4 minutes.

Given sample size 'n' = 26

The mean of the sample 'x⁻ = 21.1 min

Standard deviation of the sample 'S' = 5.4 min

The Population mean 'μ' = 18min

Step(ii):-

Null hypothesis: H₀ : The council decides that it will increase the transportation budget if the amount of waiting time for drivers exceeds 18 minutes.

'μ' > 18min

Alternative hypothesis :H₁:

'μ' <18min

Level of significance : ∝=0.05

Degrees of freedom γ = n-1 = 26-1 =25

The test statistic

`t = (x^(-)-mean )/((S)/(√(n) ) )`

`t = (21.1-18)/((5.4)/(√(26) ) )`

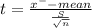
t = 2.9272

Step(iii):-

The tabulated value t = 1.708 at 25 degrees of freedom

t = 2.9272 > 1.708 at 25 degrees of freedom

Null hypothesis is rejected at 5% significance level of significance

Conclusion:-

The council decides that it will increase the transportation budget if the amount of waiting time for drivers is not exceeds 18 minutes