Question

For a certain population of men, 8 percent carry a certain genetic trait. For a certain population of women, 0.5 percent carry the same genetic trait. Let p^1 represent the sample proportion of randomly selected men from the population who carry the trait, and let p^2, represent the sample proportion of women from the population who carry the trait.

1. For which of the following sample sizes will the sampling distribution of p^1 - p^2 be approximately normal?
(A) 30 men and 30 women
(B) 125 men and 20 women
(C) 150 men and 100 women
(D) 200 men and 2,000 women
(E) 1,000 men and 1,000 women

Answer 1

(D) 200 men and 2,000 women

Explanation:

To have an approximately normal distribution for the difference between proportions, we have to have sample sizes that are big enough to satisfy this conditions:

`np>10\\\\n(1-p)>10`

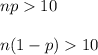
For men, we have p=0.08, so we have:

`n*0.08>10\Rightarrow n>125\\\\n(1-0.08)=n*0.92>10 \Rightarrow n>11`

The sample size for men has to be at least 125 individuals.

For women, we have p=0.005:

`n*0.005>10\Rightarrow n>2000\\\\n(1-0.005)=n*0.995>10 \Rightarrow n>11`

The sample size for women has to be at least 2000 individuals.

The option that satisfy the requirements for men and women is Option D, as the others don't have enough sample size for women.