Answer:
Negative Reciprocals
Explanation:
Consider two slopes being perpendicular to each other:
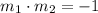
You will either receive:
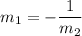
or:
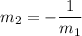
Say, you want to find perpendicular slope of 4. You have first slope as 4 and another as unknown which is assigned as m variable:
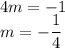
Therefore, 4 and -1/4 are perpendicular to each other. See that one slope is positives while another is negative. If you have negative slope then the perpendicular slope is positive.
Hence, they are indeed reciprocal but also negative as well.