Question

A press release states that "by an overwhelming margin, Americans want to live in a sunny place." This statement is based on data from a nationally representative sample of 2260 adult Americans. Of those surveyed, 1298 indicated that they would prefer to live in a hot climate rather than a cold climate.Do the sample data provide convincing evidence that a majority of all adult Americans prefer a hot climate over a cold climate? Test the relevant hypothesis usingα = 0.01.(Round your test statistic to two decimal places and your P-value to four decimal places.)z= P-value =

Answer 1

We conclude that majority of all adult Americans prefer a hot climate over a cold climate.

Explanation:

We are given that a press release states that "by an overwhelming margin, Americans want to live in a sunny place." This statement is based on data from a nationally representative sample of 2260 adult Americans. Of those surveyed, 1298 indicated that they would prefer to live in a hot climate rather than a cold climate.

We have to conduct a test to determine that a majority of all adult Americans prefer a hot climate over a cold climate.

Let p = proportion of all adult Americans prefer a hot climate over a cold climate.

SO, Null Hypothesis,
`H_0` : p
`\leq` 50% {means that majority of all adult Americans does not prefer a hot climate over a cold climate}

Alternate Hypothesis,
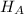`H_A` : p > 50% {means that majority of all adult Americans prefer a hot climate over a cold climate}

The test statistics that will be used here is One-sample z proportion statistics;

T.S. =
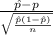`\frac{\hat p-p}{{\sqrt{(\hat p(1-\hat p))/(n) } } } }` ~ N(0,1)

where,
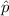`\hat p` = proportion of Americans prefer to live in a hot climate rather than a cold climate in a sample of 2260 surveyed =
`(1298)/(2260)`

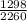
n = sample of adult Americans = 2260

So, test statistics =
`\frac{(1298)/(2260) -0.50}{{\sqrt{((1298)/(2260)(1-(1298)/(2260)))/(2260) } } } }`

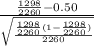
= 7.15

The value of the test statistics is 7.15.

Now, P-value of the test statistics is given by;

P-value = P(Z > 7.15) = Less than 0.0005%.

Now at 1% significance level, the z table gives critical value of 2.3263 for right-tailed test. Since our test statistics is more than the critical value of z as 2.3263 < 7.15, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.

Therefore, we conclude that majority of all adult Americans prefer a hot climate over a cold climate.