Question

An alpha particle (q = +2e, m = 4.00 u) travels in a circular path of radius 6.68 cm in a uniform magnetic field with B = 0.917 T. Calculate (a) its speed, (b) its period of revolution, (c) its kinetic energy, and (d) the potential difference through which it would have to be accelerated to achieve this energy.

Answer 1

(a) v = 2.93x10⁶ m/s

(b) T = 1.43x10⁻⁷ s

(c) K = 1.79x10⁵ eV

(d) ΔV = 89.5 kV

Step-by-step explanation:

(a) The speed of the alpha particle can be found using the magnetic force (Fm) and the centripetal force (Fc):

`Fm = Fc`

`qvB = (mv^(2))/(r)`

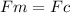
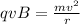
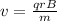`v = (qrB)/(m)` (1)

Where:

q: is the charge on the alpha particle = 2e⁻ = 2*1.602x10⁻¹⁹ C = 3.20x10⁻¹⁹ C

r: is the radius of the circular path = 6.68 cm = 6.68x10⁻² m

B: is the magnetic field = 0.917 T

m: is the mass of the alpha particle = 4.00 u = 4*1.67x10⁻²⁷ kg = 6.68x10⁻²⁷kg

Hence, the speed of the alpha particle is:

`v = (qrB)/(m) = (3.20\cdot 10^(-19) C*6.68 \cdot 10^(-2) m*0.917 T)/(6.68 \cdot 10^(-27) kg) = 2.93 \cdot 10^(6) m/s`

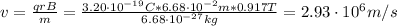
(b) The period (T) of revolution of the alpha particle is:

`T = (2\pi r)/(v) = (2\pi 0.0668 m)/(2.93 \cdot 10^(6) m/s) = 1.43 \cdot 10^(-7) s`

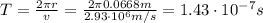
(c) The kinetic energy (K) of the alpha particle is:

`K = (1)/(2)mv^(2) = (1)/(2)6.68 \cdot 10^(-27) kg*(2.93 \cdot 10^(6) m/s)^(2) = 2.86 \cdot 10^(-14) J*(1 eV)/(1.60 \cdot 10^(-19) J) = 1.79 \cdot 10^(5) eV`

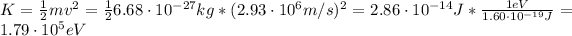
(d) The potential difference (ΔV) is:

`\Delta V = (K)/(q) = (1.79 \cdot 10^(5) eV)/(2e) = 89.5 kV`

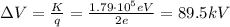
I hope it helps you!