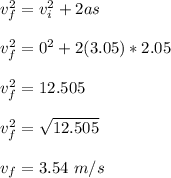Question

Two masses of 24 kg and 12 kg are suspended by a pulley that has a radius of 6.2 cm and a mass of 5 kg. The cord has a negligible mass and causes the pulley to rotate without slipping. The pulley rotates without friction. The masses start from rest 4.1 m apart. 4.1 m 6.2 cm 5 kg ω 24 kg 12 kg Determine the speeds of the two masses as they pass each other. Treat the pulley as a uniform disk. The acceleration of gravity is 9.8 m/s 2 . Answer in units of m/s.

Answer 1

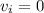`v_i =0` since the mass start at rest

`v_f = 3.54 \ m/s`

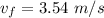
Step-by-step explanation:

Given that :

Two masses of 24 kg and 12 kg are suspended by a pulley

so; let
`m_1` = 24 kg and
`m_2` = 12 kg

radius r = 6.2 cm

mass M = 5.0 kg

The moment of inertia on the pulley is ;

`I = (1)/(2)Mr^2`

For the force equation with mass m ; we have:

`m_1g -T_1 = m_1a`

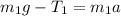
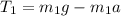`T_1 =m_1g-m_1a` -------- Equation (1)

Force equation of the mass
`m_2` can be written as:

`T_2 -m_2g = m_2a`

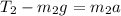
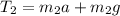`T_2 = m_2a+m_2g` -------- Equation (2)

The torque on the pulley is expressed as:

`(T_1-T_2) r = I \alpha`

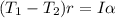
where
`a= r* \alpha`

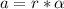
Then;

`(T_1-T_2) r =(1)/(2)Mr^2 (a)/(r)`

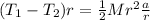
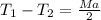`T_1 -T_2 = \frac {Ma}{2}` ----- Equation (3)

Replacing equation (1) and (2) into equation (3) ; we have:

`(m_1g -m_1a) -(m_2g + m_2a) = (Ma)/(2)`

`(24*9.8 -24a) -(12*9.8 + 12a) = (5a)/(2)`

`235.2 - 24a - 117.6-12a = (5a)/(2)`

`117.6 - 36a= (5a)/(2)`

`2(117.6-36a)= (5a)/(2)`

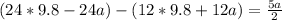
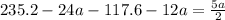
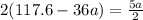
235.2 - 72a = 5a

235.2 = 5a + 72a

235.2 = 77a

a =
`(235.2)/(77)`

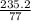
a= 3.05 m/s²

Let's consider the mass
`m_1` of the motion, with initial velocity

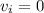`v_i =0` since the mass start at rest

distance traveled (s) = 2.05 m

acceleration = 3.05 m/s²

Using the formula:

`v_f^2 = v_i^2 + 2 as \\ \\ v_f^2 =0^2+2(3.05)*2.05 \\ \\ v_f^2 = 12.505 \\ \\ v^2_f = √(12.505) \\ \\ v_f = 3.54 \ m/s`