Question

The thickness of metal wires used in the manufacture of silicon wafers is assumed to be normallydistributed with meanμ. To monitor the production process, the thickness of 40 wires is taken. Theoutput is considered unacceptable if the mean differs from the target value of 10. The 40 measurementsyield a sample mean of 10.2 and sample standard deviation of 1.2. Conduct the appropriate hypothesistest with a significance level ofα= 0.05.

(a) State the Null hypothesis.
(b) State the Alternative Hypothesis.
(c) Give the formula for the test statistic and the reference distribution.
(d) Calculate the test statistic.
(e) Calculate the p-value.
(f) What implication does this test have for the production process?

Answer 1

(a) Null Hypothesis,
`H_0` :
`\mu` = 10

(b) Alternate Hypothesis,
`H_A` :
`\mu\\eq` 10

(c) One-sample t test statistics distribution : T.S. =
`(\bar X -\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

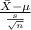(d) The value of the test statistic is 1.054.

(e) The p-value = 0.1493

(f) We conclude that the mean equals the target value of 10 which means that the output can be considered acceptable as it doesn't differs from the target value of 10.

Explanation:

We are given that the thickness of metal wires used in the manufacture of silicon wafers is assumed to be normally distributed with mean μ. To monitor the production process, the thickness of 40 wires is taken.

The output is considered unacceptable if the mean differs from the target value of 10. The 40 measurements yield a sample mean of 10.2 and sample standard deviation of 1.2.

Let
`\mu` = mean thickness of metal wires used in the manufacture of silicon wafers.

(a) Null Hypothesis,
`H_0` :
`\mu` = 10 {means that the mean equals the target value of 10}

(b) Alternate Hypothesis,
`H_A` :
`\mu\\eq` 10 {means that the mean differs from the target value of 10}

(c) The test statistics that will be used here is One-sample t test statistics as we don't know about the population standard deviation;

T.S. =
`(\bar X -\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

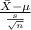where,
`\mu` = sample mean = 10.2

s = sample standard deviation = 1.2

n = sample of yields = 40

(d) So, test statistics =
`(10.2-10)/((1.2)/(√(40) ) )` ~
`t_3_9`

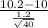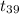
= 1.054

The value of the test statistic is 1.054.

(e) Now, P-value of the test statistics is given by;

P-value = P(
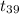`t_3_9` > 1.054) = 0.1493

Now at 0.05 significance level, the t table gives critical values between -2.0225 and 2.0225 at 39 degree of freedom for two-tailed test. Since our test statistics lies within the critical values of t, so we have insufficient evidence to reject our null hypothesis as it will not fall in the rejection region due to which we fail to reject our null hypothesis.

(e) Therefore, we conclude that the mean equals the target value of 10 which means that the output can be considered acceptable as it doesn't differs from the target value of 10.