Question

An xyz-coordinate system has an x-axis, a y-axis, and a vertical positive z-axis. A right circular cone labeled z = 26 - √( x² + y²) has a circular base in the xy-plane that is a circle centered at (0, 0, 0) and a vertex on the positive z-axis.

Find the volume of the solid bounded by the surface z = ​f(x,y) and the​ xy-plane.
(Type an exact​ answer, using pi as​ needed.)

Answer 1

V = 5858.66π

Explanation:

This problem can be solved by using the washer method in the integration.

If you assume that the lateral of the cone is given by a line equation of the form:

`z=(r)/(h)u`

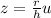
r: radius of the cone = 26 (because for z=0 -> √( x² + y²) = 26 = r)

h: height of the cone = 26 (because for x=0 and y=0, z = 26)

you can integrate in the following form to get the volume of the cone:

`V=\pi\int_0^(26)[(r)/(h)u]^2du=\pi(r^2)/(h^2)[(u^3)/(3)]\\\\V=\pi((26)^2)/((26)^2)((26)^3)/(3)=5858.66\pi`

hence, the volume of the cone is 5858.66π