Question

A 1,000g of C-14 is left to decay radioactively. The half-life of Carbon-14 is approximately 5,700 years. What fraction of the sample will remain after 17,100 years?

Answer 1

Answer: The fraction that is left is
`(1)/(8)`

Step-by-step explanation:

Expression for rate law for first order kinetics is given by:

`t=(2.303)/(k)\log(a)/(a-x)`

where,

k = rate constant

t = age of sample

a = let initial amount of the reactant

a - x = amount left after decay process

a) for completion of half life:

Half life is the amount of time taken by a radioactive material to decay to half of its original value.

`t_{(1)/(2)}=(0.693)/(k)`

`k=(0.693)/(5700years)=0.00012years^(-1)`

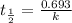
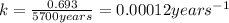
b) for 17100 years

`t=(2.303)/(k)\log(1000)/(a-x)`

`17100=(2.303)/(0.00012)\log(1000)/(a-x)`

`\log(1000)/(a-x)=0.89`

`(1000)/(a-x)=7.8`

`(a-x)=125g`

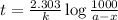
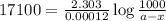
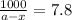
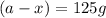
Fraction of the sample remained =
`(125)/(1000)=(1)/(8)`

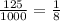
The fraction that is left is
`(1)/(8)`