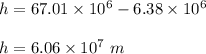Step-by-step explanation:
Given that,
A satellite that goes around the earth once every 24 hours is called a geosynchronous satellite, T = 24 hours = 86400 s
We need to find the radius R of the orbit of a geosynchronous satellite that circles the earth. It can be calculated using Kepler's third law of motion as :

R is the distance from the center of the earth.
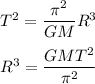
G is universal gravitational constant
M is mass of earth

So, the satellite distance from the earth's surface is :