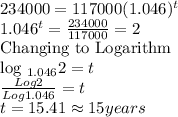Question

The number of applications for​ patents, N, grew dramatically in recent​ years, with growth averaging about 4.6​% per year. That​ is, Upper N prime (t )equals0.046Upper N (t ). ​a) Find the function that satisfies this equation. Assume that tequals0 corresponds to 1980​, when approximately 117 comma 000 patent applications were received. ​b) Estimate the number of patent applications in 2025. ​c) Estimate the doubling time for Upper N (t ).

Answer 1

(a)
`N(t)=117000(1.046)^t`

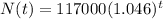
(b)885,343

(c)15 years

Explanation:

Given that the number of applications for​ patents, N, grew dramatically in recent​years, with growth averaging about 4.6​% per year.

Part A

The function which satisfies the equation given that that t = 0 corresponds to 1980​, when approximately 117,000 patent applications were received is given by:

`N(t)=117000(1+0.046)^t\\N(t)=117000(1.046)^t`

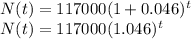
where:

• N(t) is the number of patent applications received at any particular year,
• t is the number of years after 1980.

Part B

In 2025, there are 2025 - 1980 = 45 years after 1980.

The number of patent applications 45 years after 1980 is given by:

`N(t)=117000(1.046)^t\\N(45)=117000(1.046)^(45)\\\approx 885343`

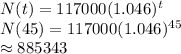
Part C

The doubling time for N(t) is the time it takes the number of patents to be

2 X 117,000 = 234,000

When N(t)=234000

`234000=117000(1.046)^t\\1.046^t=(234000)/(117000) =2\\$Changing to Logarithm\\log _(1.046)2=t\\(Log 2)/(Log 1.046)=t\\ t=15.41\approx 15 years`