Answer:
a) -4
b) 1
c) 1
Explanation:
a) The matrix A is given by:
![A=\left[\begin{array}{ccc}-3&0&1\\2&-4&2\\-3&-2&1\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/2r1qwurxd3j5br6imrjnftmlotxlevk2sb.png)
to find the eigenvalues of the matrix you use the following:
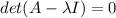
where lambda are the eigenvalues and I is the identity matrix. By replacing you obtain:
![A-\lambda I=\left[\begin{array}{ccc}-3-\lambda&0&1\\2&-4-\lambda&2\\-3&-2&1-\lambda\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/o4ygh9w6dnc1vpbdcc1ypuwdyjiw4rvkyc.png)
and by taking the determinant:
![[(-3-\lambda)(-4-\lambda)(1-\lambda)+(0)(2)(-3)+(2)(-2)(1)]-[(1)(-4-\lambda)(-3)+(0)(2)(1-\lambda)+(2)(-2)(-3-\lambda)]=0\\\\-\lambda^3-6\lambda^2-12\lambda-16=0](https://img.qammunity.org/2021/formulas/mathematics/high-school/6y0bxwail7lopqlhnedatdscux0i1442zg.png)
and the roots of this polynomial is:

hence, the real eigenvalue of the matrix A is -4.
b) The multiplicity of the eigenvalue is 1.
c) The dimension of the eigenspace is 1 (because the multiplicity determines the dimension of the eigenspace)