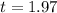Question

At a canning facility, a technician is testing a machine that is supposed to deliver 250 milliliters of product. The technician tests 44 samples and determines the volume of each sample. The 44 samples have a mean volume of 251.6 mL. The machine is out of calibration when the average volume it dispenses differs significantly from 250 mL. The technician wants to perform a hypothesis test to determine whether the machine is out of calibration. Assume σ = 5.4 is known. Compute the value of the test statistic.

Answer 1

The value of the test statistic is
`t = 1.97`

Explanation:

The null hypothesis is:

`H_(0) = 250`

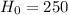
The alternate hypotesis is:

`H_(1) \\eq 250`

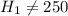
Our test statistic is:

`t = (X - \mu)/((\sigma)/(√(n)))`

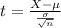
In which X is the sample mean,
`\mu` is the null hypothesis value,
`\sigma` is the standard deviation and n is the size of the sample.

In this problem:

`X = 251.6, \mu = 250, \sigma = 5.4, n = 44`

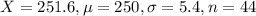
So

`t = (X - \mu)/((\sigma)/(√(n)))`

`t = (251.6 - 250)/((5.4)/(√(44)))`

`t = 1.97`

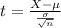
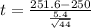
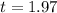
The value of the test statistic is
`t = 1.97`