Question

10) David rode his bike 17 miles from his home to Columbus, Ohio and then completed

the 53 miles trip by car from Columbus to Mansfield, Ohio. Assume that the average rate
of the car was 43 mph faster than the average rate of the bike. Find the bike's rate if the
total time for the trip was 1 hour and 40 minutes.

Answer 1

Answer: The average speed on bike is 20.57 mph and the average speed on car is 63.57 mph.

Explanation:

David did 17 miles on bike and 53 miles on car.

The average speed of the car was 53 mph faster than the average speed on bike.

The total time of the traavle was 1 hour and 40 minutes.

Let's write this in hours:

We know that a hour has 60 minuts, then 40 minuts is equal to:

a = 40/60 = 2/3 = 0.66

Then one hour and 40 minutes is equal to 1.66 hours.

Let's call Sb to the speed of the car and Sc to the speed of the car.

We have that:

Sc = Sb + 43mi/h.

We have that the time will neded to travel a given distance is equal to the distance divided the average speed.

Then we have that:

(17 mi)/Sb + (53mi)/Sc = 1.66 h

Now, we can replace Sc with the previous equation and solve it for Sb

(17 mi)/Sb + (53mi)/(Sb + 43mi/h) = 1.66 h

I will remove the units, so it is easier to read:

17/Sb + 53/(Sb + 43) = 1.66

We multiply both sides by (Sb + 43)

(Sb + 43)*17/Sb + 53 = 1.66*(Sb + 43) = 1.66 + 71.38

17 + 43*17/Sb + 53 = 1.66*Sb + 71.38

(731)/Sb = 1.66*Sb + 1.38

we multiply both sides by Sb

731 = 1.66*Sb^2 + 1.38*Sb

Now we need to solve this quadratic equation:

1.66*Sb^2 + 1.38*Sb - 731 = 0

the roots are:

`Sb = (-1.38 +- √(1.38^2 -4*1.66*(-731)) )/(2*1.66) = (-1.38 +- 69.68 )/(3.32)`

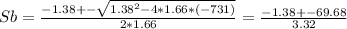
We have two roots, one positive and one negative, we need to choose the positive one because average speed must be a positive number.

Sb = (-1.38 + 69.68)/3.32 = 20.57

Then the speed on bike is 20.57 miles per hour.

And the speed on the car is:

20.57 mph + 43 mph = 63.57 mph