Answer:
The ratio of surface areas is 36:121.
Explanation:
We have, the ratio of the heights of two similar solids is 6:11. It is required to find the ratio of their surface areas. As the two solids are similar, it means that the ratio of surface areas of solids is directly proportional to the square of their heights such that,
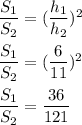
So, the ratio of surface areas is 36:121.