Answer:
y =
 x -
x -
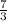
Explanation:
Given
So we will set up a set values of t to have x
t = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
<=> x = {4, 1, -2, -5, -8, -11, -14, -17, -20, -23, -26}
So we will set up a set values of t to have y
t = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
<=.> y = {-5, -3, -1, 1, 3, 5, 7, 9, 11, 13, 15}
At the end, we have the table of values of x and y as following:
x = {4, 1, -2, -5, -8, -11, -14, -17, -20, -23, -26}
y = {-5, -3, -1, 1, 3, 5, 7, 9, 11, 13, 15}
Let find the slope of the linear equation:
m =
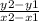
<=> m =
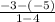 =
=

and the standard form of a linear equation is:
y= mx + b
In this situation, y =
 x + b (1)
x + b (1)
Because the line goes through point (4, -5), so we substitute it into (1) to find b.
<=> -5 =
 *4 + b
*4 + b
<=> b = -
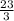
<=> y =
 x -
x -
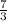
Please have a look at the attach photo.
Hope it will find you well.