Question

A researcher wants to determine if bodybuilders on anabolic steroids are stronger or weaker than chess players. To test this, a random sample of 37 chess players and 32 body builders on anabolic steroids were asked to perform their "one rep" maximum bench press. According to the hypothesis test, the best decision was to reject the null hypothesis. Given μ1 represents the body builders on anabolic steroids and μ2 represents the chess players, which is the best conclusion?

Answer 1

Null hypothesis:
`\mu_1 \geq \mu_2`

Alternative hypothesis:
`\mu_1 <\mu_2`

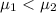
since the decision for this case is reject the null hypothesis then we can conclude that the claim for this case makes sense since we reject the null hypothesis we have enough evicende at a significance level given that the anabolic players are stronger than the chess players

Explanation:

We have the following info given:

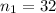`n_1 =32` represent the sample size for body builders

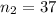`n_2 =37` represent the sample size for chess players

We define the following notation:

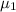`\mu_1` represent the true mean for body builders on anabolic steroids

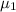`\mu_1` represent the true mean for chess players

And we want to determine if bodybuilders on anabolic steroids are stronger or weaker than chess players ([\tex] \mu_1 < \mu_2[/tex]) in the alternative hypothesis and in the null hypothesis we will have the complement rule, and the best system of hypothesis are:

Null hypothesis:
`\mu_1 \geq \mu_2`

Alternative hypothesis:
`\mu_1 <\mu_2`

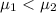
since the decision for this case is reject the null hypothesis then we can conclude that the claim for this case makes sense since we reject the null hypothesis we have enough evicende at a significance level given that the anabolic players are stronger than the chess players