Answer:
The standard deviation of the number of dogs who weigh 65 pounds or more is 1.93.
Explanation:
For each dogs, there are only two possible outcomes. Either they weigh less than 65 pounds, or they weight at least 65 pounds. The probability of a dog weighing more than 65 pounds is independent of other dogs. So we use the binomial probability distribution to solve this question.
Binomial probability distribution
Probability of exactly x sucesses on n repeated trials, with p probability.
The standard deviation of the binomial distribution is:
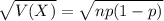
It is estimated that 45% of adult Australian sheep dogs weigh 65 pounds or more.
This means that

Sample of 15 adult dogs is studied.
This means that

What is the standard deviation of the number of dogs who weigh 65 pounds or more
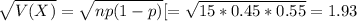
The standard deviation of the number of dogs who weigh 65 pounds or more is 1.93.