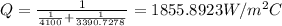Question

11–17 A long, thin-walled double-pipe heat exchanger with tube and shell diameters of 1.0 cm and 2.5 cm, respectively, is used to condense refrigerant-134a with water at 20°C. The refrigerant flows through the tube, with a convection heat transfer coefficient of hi = 4100 W/m2·K. Water flows through the shell at a rate of 0.3 kg/s. Determine the overall heat transfer coefficient of this heat exchanger.

Answer 1

the overall heat transfer coefficient of this heat exchanger is 1855.8923 W/m²°C

Step-by-step explanation:

Given:

d₁ = diameter of the tube = 1 cm = 0.01 m

d₂ = diameter of the shell = 2.5 cm = 0.025 m

Refrigerant-134a

20°C is the temperature of water

h₁ = convection heat transfer coefficient = 4100 W/m² K

Water flows at a rate of 0.3 kg/s

Question: Determine the overall heat transfer coefficient of this heat exchanger, Q = ?

First at all, you need to get the properties of water at 20°C in tables:

k = 0.598 W/m°C

v = 1.004x10⁻⁶m²/s

Pr = 7.01

ρ = 998 kg/m³

Now, you need to calculate the velocity of the water that flows through the shell:

`v_(w) =(m)/(\rho \pi ((d_(2)^(2)-d_(1)^(2) )/(4) )) =(0.3)/(998*\pi ((0.025^(2)-0.01^(2) )/(4)) ) =0.729m/s`

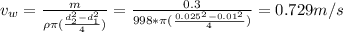
It is necessary to get the Reynold's number:

`Re=(v_(w)(d_(2)-d_(1)) )/(v) =(0.729*(0.025-0.01))/(1.004x10^(-6) ) =10891.4343`

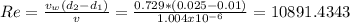
Like the Reynold's number is greater than 10000, the regime is turbulent. Now, the Nusselt's number:

`Nu=0.023Re^(0.8) Pr^(0.4) =0.023*(10891.4343)^(0.8) *(7.01)^(0.4) =85.0517`

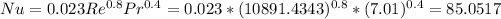
The overall heat transfer coefficient:

`Q=(1)/((1)/(h_(1) )+(1)/(h_(2) ) )`

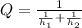
Here

`h_(2) =(kNu)/(d_(2)-d_(1)) =(0.598*85.0517)/(0.025-0.01) =3390.7278W/m^(2)C`

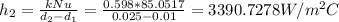
Substituting values:

`Q=(1)/((1)/(4100)+(1)/(3390.7278) ) =1855.8923W/m^(2) C`