Question

Kids with cell phones: A marketing manager for a cell phone company claims that less than 58% of children aged 8-12 have cell phones. In a survey of 820 children aged 8-12 by a national consumers group,

asked Jul 28, 2021 184k views

1 Answer

Ask a Question

Jassen · Answer 1 · 2021-08-04T05:21:54+0000

Answer:

$z=\frac{0.54 -0.58}{\sqrt{(0.58(1-0.58))/(820)}}=-2.32$

p_v =P(z<-2.32)=0.0102

Since the p value is lower than the significance level
$\alpha=0.1$ we have enough evidence to reject the null hypothesis and the claim for the manager makes sense.

For the Ti84 preocedure we need to do this:

STAT> TESTS> 1-Z prop Test

And then we need to input the following values:

po= 0.58

x = 443 , n= 820

prop <po

And then calculate and we will get the same results

Explanation:

Data given and notation

n=820 represent the random sample taken

X=443 represent the people that had cell phones

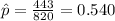$\hat p=(443)/(820)=0.540$ estimated proportion of people that had cell phones

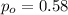p_o=0.58 is the value that we want to test

$\alpha=0.1$ represent the significance level

Confidence=90% or 0.90

z would represent the statistic (variable of interest)

p_v represent the p value (variable of interest)

System of hypothesis

We need to conduct a hypothesis in order to test the claim that the true proportion is less than 0.58.:

Null hypothesis:
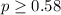
$p\geq 0.58$

Alternative hypothesis:
p < 0.58

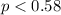
The statistic is given by:

$z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}$ (1)

And replacing we got:

Since we have all the info requires we can replace in formula (1) like this:

$z=\frac{0.54 -0.58}{\sqrt{(0.58(1-0.58))/(820)}}=-2.32$

Decision

The significance level provided
$\alpha=0.1$ . Now we can calculate the p value

Since is a left tailed test the p value would be: