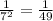Question

Simplify the following expression

Answer 1

Answer: C)
`(1)/(49)`

Explanation:

`7^-^(5)/(6)*7^-^(7)/(6)`

In order to make our exponents positive, we use a rule that says that if we have:
`a^-1=(1)/(a^1)`

`(1)/(7^(5)/(6) )*(1)/(7^(7)/(6) )`

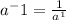
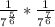
We have the same base 7, we only have to add the exponents.

`(1)/(7^(5)/(6)^+^(7)/(6) )`

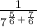
I'm going to solve the denominator separately so that you don't have to struggle to see the small numbers.

`(5)/(6)+(7)/(6)=(12)/(6)=2`

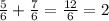
The resulting fraction is:

`(1)/(7^2) =(1)/(49)`

Answer 2

C

Explanation: