Question

A soccer ball was kicked in the air and follows the path h(x)=−2x2+1x+6, where x is the time in seconds and h is the height of the soccer ball. At what time will the soccer ball hit the ground?

Answer 1

At the time x = 2 seconds

Explanation:

The height of the soccer ball is described by the function h(x), so if we want to know when the soccer ball will hit the ground, we just need to find the value of x that gives us the height zero, that is, h(x) = 0:

h(x) = −2*x^2 + 1*x + 6

0 = −2*x^2 + x + 6

2*x^2 - x - 6 = 0

Using Bhaskara's formula, we have:

Delta = b^2 - 4ac = 1 + 48 = 49

sqrt(Delta) = 7

x = (-b + sqrt(Delta)) / 2a = (1 + 7) / 4 = 2 seconds

Answer 2

x= 2 seconds

Explanation:

Hello, I can help you with this

Step one

check the data

soccer ball was kicked in the air and follows the path h(x)=−2x2+1x+6

h(x)=−2x2+1x+6,using the correct format

`h(x)= -2x^(2) +x+6`

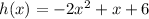
where

x is the time in seconds

and

h is the height of the soccer ball

so, when the ball hit the ground its height is o (zero)

you need put this value into the equation and then isolate x to find its value.

Step two

find the value of x, when h=0

`h(x)= -2x^(2) +x+6\\0=-2x^(2) +x+6\\using\\x=\frac{-b+\sqrt{ b^(2)-4ac }}{2a}\\ a=-2,b=1,c=6\\x=\frac{-1+\sqrt{ 1^(2)-4(-2)(6) }}{2*-2}\\x=\frac{-1+\sqrt{ 1^(2)+48}}{-4}\\x=(-1+√(49))/(-4)\\x_(1) =(-1+7)/(-4)\\x_(2) =(-1-7)/(-4)\\x_(1) =-(3)/(2) \\x_(2) =(-8)/(-4) \\x_(2)=2`

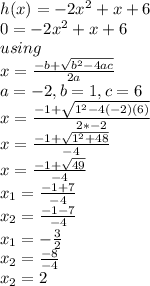
we are looking for a time, so we only are going to use the positive x, it is X2

x= 2 sec

have a good day.