Question

A hydraulic jump is induced in an 80 ft wide channel. The water depths on either side of the jump are 1 ft and 10 ft. Please calculate: a) The velocity of the faster moving flow. b) The flow rate (discharge). c) The Froude number of the sub-critical flow. d) The flow energy dissipated in the hydraulic jump (expressed as percentage of the energy prior to the jump). e) The critical depth.

Answer 1

a) The velocity is 42.0833 ft/s

b) The flow rate is 3366.664 ft³/s

c) The Froude number is 0.2345

d) The flow energy dissipated (expressed as percentage of the energy prior to the jump) is 18.225 ft

e) The critical depth is 3.8030 ft

Step-by-step explanation:

Given data:

80 ft wide channel, L

1 ft and 10 ft water depths, d₁ and d₂

Questions: a) Velocity of the faster moving flow, v = ?

b) The flow rate (discharge), q = ?

c) The Froude number, F = ?

d) The flow energy dissipated, E = ?

e) The critical depth, dc = ?

a) For the velocity:

`(d_(2) )/(d_(1) ) =(1)/(2) (\sqrt{1+8F^(2) } -1)`

`10*2=\sqrt{1+8F^(2) } -1`

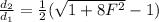
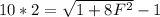
Solving for F:

F = 7.4162

`v=F\sqrt{gd_(1) }`

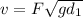
Here, g = gravity = 32.2 ft/s²

`v=7.4162*√(32.2*1) =42.0833ft/s`

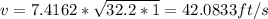
b) The flow rate:

`q=v*L*d_(1) =42.0833*80*1=3366.664ft^(3) /s`

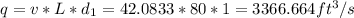
c) The Froude number:

`v_(2) =(q)/(L*d_(2) ) =(3366.664)/(80*10) =4.2083ft/s`

`F=\frac{v_(2)}{\sqrt{gd_(2) } } =(4.2083)/(√(32.2*10) ) =0.2345`

d) The flow energy dissipated:

`E=((d_(2)-d_(1))^(3) )/(4d_(1)d_(2)) =((10-1)^(3) )/(4*1*10) =18.225ft`

e) The critical depth:

`d_(c) =((((q)/(L))^(2) )/(g) )^(1/3) =((((3366.664)/(80))^(2) )/(32.2) )^(1/3) =3.8030ft`