Given:
Given that the circle is inscribed in a polygon ELPJ.
The lengths of the sides EK = 2, LU = 4, PV = 1 and JS = 2.
We need to determine the perimeter of ELPJ.
Lengths of the sides:
We need to determine the lengths of the sides ES, LK, PU and JV.
We know the theorem that "the lengths of the two tangents drawn from the an exterior point to a circle are equal".
Hence, using this theorem, we have;
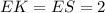

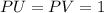
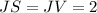
Perimeter of ELPJ:
The perimeter of ELPJ is given by
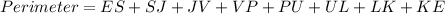
Substituting the values, we have;
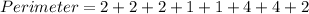
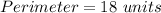
Thus, the perimeter of ELPJ is 18 units.