Question

A regulation baseball can weigh no more than 149 grams. A factory produces baseballs with weights that are normally distributed with a mean of 146 grams and a standard deviation of 2.3 grams. (a) If a baseball produced by the factory is randomly selected, what is the probability that it is within regulation weight

Answer 1

The probability that a randomly selected baseball is within the regulation weight is 0.9032.

Explanation:

Mean weight of the baseballs = μ = 146 grams

Standard Deviation = σ = 2.3 grams

A regular baseball can weight no more than 149 grams. We have to find the probability that a randomly selected baseball is within the regulation weight i.e. it weights no more than 149 gram. Therefore, the weight of baseball should be equal to or less than 149 grams.

Since, the weights of baseball are Normal Distributed and we have the value of Population standard deviation, we will use z-distribution to find the desired probability.

First we will convert the given weight to its equivalent z-score, then using the z-table we will find the desired probability. The formula to calculate the z-score is:

`z=(x-\mu)/(\sigma)`

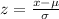
x = 149 converted to z-score will be:

`z=(149-146)/(2.3)=1.30`

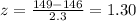
The probability that the weight of baseball is equal to or less than 149 is equivalent to the probability of z score being less than or equal to 1.30.

i.e.

P(X ≤ 149) = P(z ≤ 1.30)

From the z-table we can find this probability:

P(z ≤ 1.30) = 0.9032

This means,

P(X ≤ 149) = P(z ≤ 1.30) = 0.9032

Therefore, the probability that a randomly selected baseball is within the regulation weight is 0.9032.