Answer:
This means that the first interval, with 9000 viewers, is 3 times as narrower as the second interval, with 1000 viewers.
Step-by-step explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.

In which
z is the zscore that has a pvalue of
 .
.
The width of the interval is:
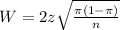
In this sample:
Two 90% intervals, with different lenghts. So both have the same values for z an

Interval A:
9000 viewers.
So the width is
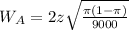
Interval B:
100 viewers
So the width is
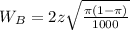
Relationship between the widths:
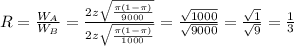
This means that the first interval, with 9000 viewers, is 3 times as narrower as the second interval, with 1000 viewers.