Question

The length of a rectangle is 3 cm greater than the width of the rectangle.

If the area of the rectangle is 40 square cm, what is the length of the
rectangle?
A) 5 cm
B) 8 cm
C) 11 cm
D) 17 cm

Answer 1

B) 8 cm

Explanation:

Hello, I can help you with this

according to the question

The length of a rectangle is 3 cm greater than the width of the rectangle.

convert this into algebraic terms

Step 1

do the eqution

Let

W,width

L,Length

The length of a rectangle(L) is(=) 3 cm greater than the width (W+3) of the rectangle.

note:3 cm greater than the width (W+3) means that you need add 3 to the width to obtain the length

L=W+3 equation(1)

the area of the rectangle is 40 square cm

Let

A,Area

Area= 40 cm

A=40

also,A=L*W

40=L*W equation(2)

Step 2

solve the equations

L=W+3 equation(1)

40=L*W equation(2)

replace the value of L from equaiton (1) into equation (2)

`40=(W+3)*W\\40=W^(2) +3W\\W^(2) +3W-40=0\\W^(2)+3W-40=0\\\\use cuadratic\\\\w=\frac{-b+-\sqrt{b^(2)-4ac } }{2a}\\\\w=\frac{-3+-\sqrt{3^(2)-4*1*-40 } }{2*1}\\w=(-3+-√(169) )/(2)\\`

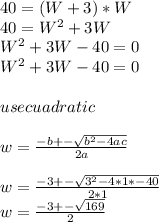
we are looking for a distance, so we need the positive valur only.

`w=(-3+-√(169) )/(2)\\\\w=(-3+13)/(2)\\ w=5\\`

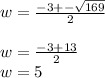
Step 3

Now, replace the value of W into equation (1) to obtain the length

L=W+3 equation(1)

L=5+3

L=8

so, the length is 8 cm, B) 8 cm

Have a nice day.